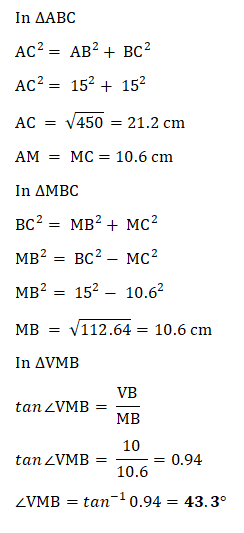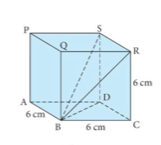
a) BD
    b) AS
    c) BS
    d) the angle SBD
    e) the angle ASB.

(a)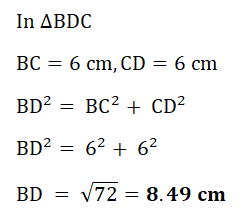
(b)
(c)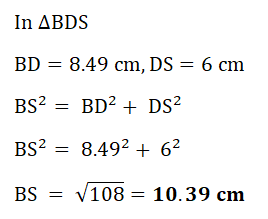
(d)
(e)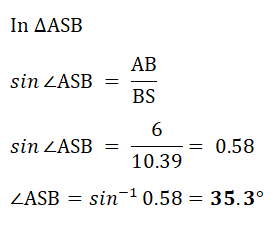

2. In the wedge shown, PQRS is perpendicular to ABRQ. 
    PQRS and ABRQ are rectangles with AB = QR = 6 m, BR = 4 m, RS = 2 m. Find :

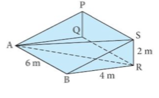   a) BS
   b) AS
   c) Angle BSR
   d) Angle ASR
   e) Angle PAS

(a)	PQRS is perpendicular to ABRQ Hence SR is perpendicular to BR
(b)	ABRQ is a rectangle. Hence ∠ABR = 90°
(c)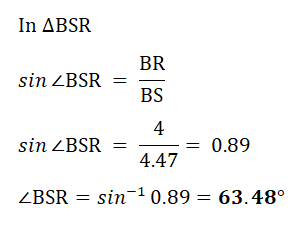
(d)
(e)

3. In the diagram A, B and O are points in a horizontal plane and P is vertically above O.
   OP = h m. A is due West of O, B is due South of O and AB = 60 m. 
   The angle of elevation of P from A is 25° and the angle of elevation of P from B is 33°. 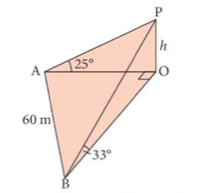a) Find the length AO in terms of h.
 b) Find the length of BO in terms of h.
 c) Find the value of h.

(a)	In △ AOP, ∠AOP = 90°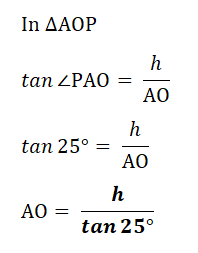
(b)	In △BPO, ∠BOP = 90°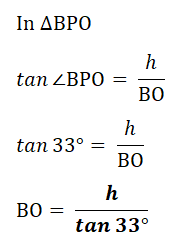
(c)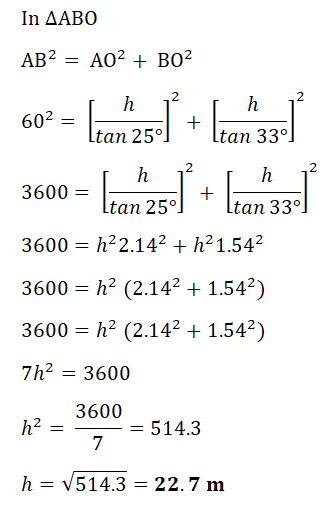

4. An observer at the top of a tower of height 15 m sees a man due West of him at an angle of depression of 31°. 
    He sees another man due South at an angle of depression 17°. 
  

  Find the distance between the men.

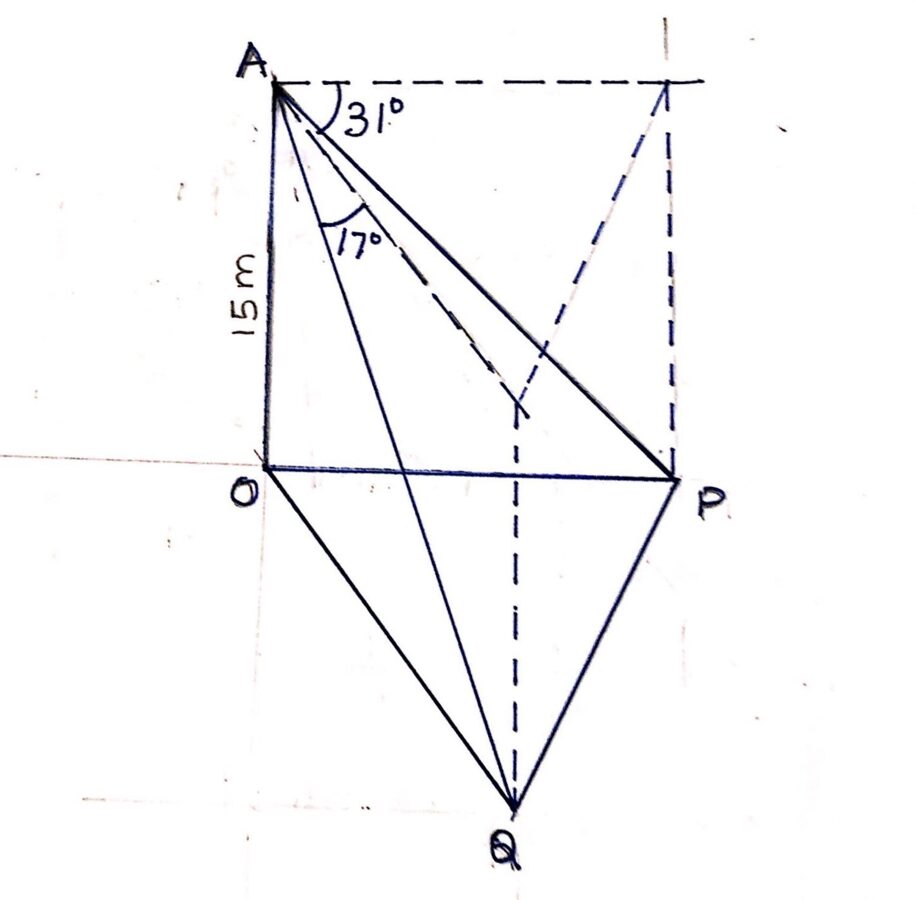Let Tower = OA = 15 m Man due West = P Angle of depression = 31° Hence angle with tower = 59° Man due South = Q Angle of depression = 17° Hence angle with tower = 73° Distance between men = PQ OP is west and OQ south. ∠POQ = 90°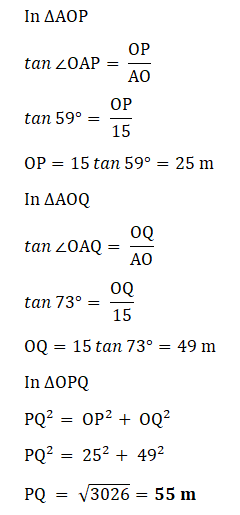

5. The figure shows a triangular pyramid on a horizontal base ABC. 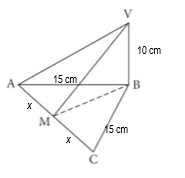    V is vertically above B where VB = 10 cm, Angle ABC = 90° and AB = BC = 15 cm. 
    Point M is the mid-point of AC. Calculate the size of angle VMB.

V Is vertically above B.
Hence VBA id perpendicular to ABC