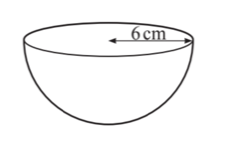
Calculate the volume.
Give the units of your answer.
(The volume, V, of s sphere with radius r is V = 4/3πr³)
 b). The diagram shows a prism ABCDEF.
b). The diagram shows a prism ABCDEF.
The cross-section is a right angled triangle BCD.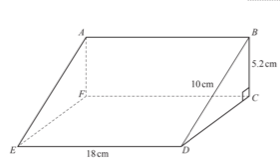 BD = 10 cm, BC = 5.2 cm and ED = 18 cm.
BD = 10 cm, BC = 5.2 cm and ED = 18 cm.
(i) a) Work out the volume of the Prism.
b) Calculate the angle BEC
c) The point G lies on the line ED and GD = 7 cm. Work out angle BGE
(Cambridge Assessment International Education. 0580/42, October/November 2019, Q 4)
| (a) | 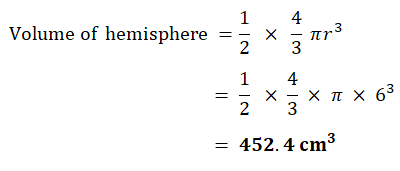 |
| (b)(i)a | 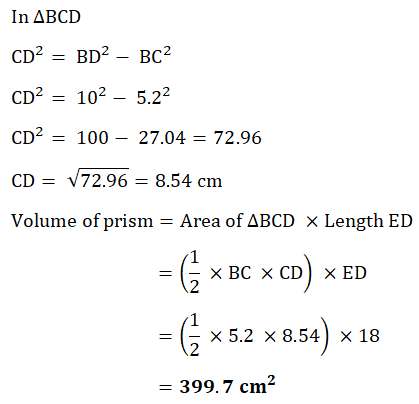 |
| (b)(i)b |  |
| (b)(i)c | 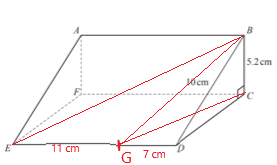   |
2. The diagram shows a sector of a circle of radius 3.8 cm.
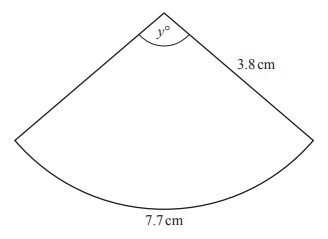
(Cambridge Assessment International Education. 0580/42, May/June 2019, Q 8b)
| (i) | 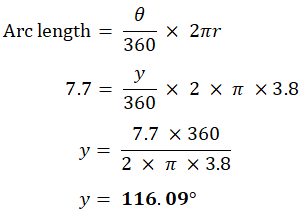 |
| (ii) | 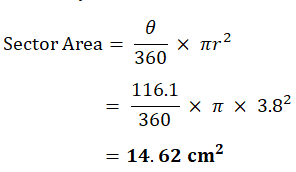 |
(i) Calculate the radius of the sphere.
(The volume, V, of a sphere with radius r is V = 4/3πr³)
(ii) The metal sphere is placed in an empty tank.
The tank is a cylinder with radius 50 cm, standing on its circular base.
Water is poured into the tank to a depth of 60 cm.
Calculate the number of litres of water needed.
(b) A different tank is a cuboid measuring 1.8 m by 1.5 m by 1.2 m.
Water flows from a pipe into this empty tank at a rate of 200 cm³ per second.
Find the time it takes to fill the tank. Give your answer in hours and minutes.
(Cambridge Assessment International Education. 0580/42, May/June 2019, Q 10)
| (a)(i) | 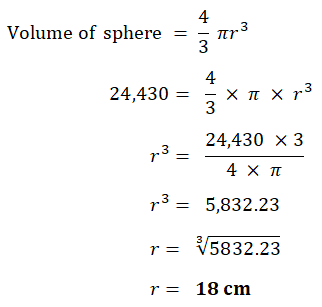 |
| (a)(ii) |  |
| (b) |  |
 (Cambridge Assessment International Education. 0580/22, May/June 2019, Q 7)
(Cambridge Assessment International Education. 0580/22, May/June 2019, Q 7) 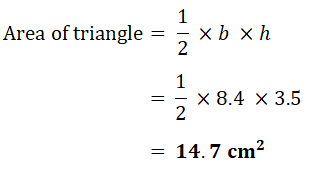 |
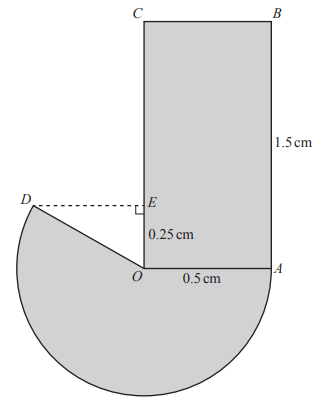 The circle has centre O and radius OA.
OA = OD = 0.5 cm and AB = 1.5 cm.
The circle has centre O and radius OA.
OA = OD = 0.5 cm and AB = 1.5 cm. E is a point on OC such that OE = 0.25 cm and angle OED = 90°.
(a) Calculate the perimeter of the logo.
(b) Calculate the area of the logo
(c) A mathematically similar logo is drawn.
This gold model is 15 mm thick. One cubic centimetre of gold has a mass of 19 grams.
Calculate the mass of the gold model in kilograms.
(Cambridge Assessment International Education. 0580/42, February/March 2019, Q 6)
| (a) |   |
| (b) | 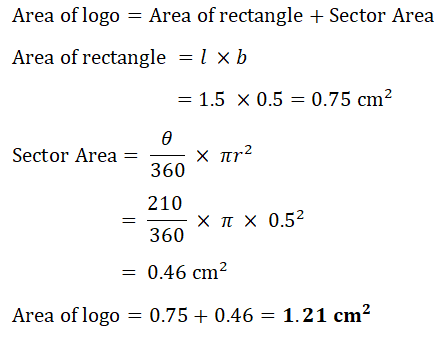 |
| (c)(i) | 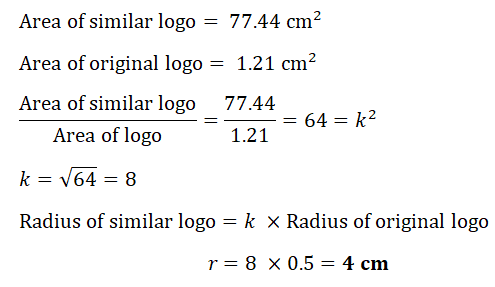 |
| (c)(ii) | 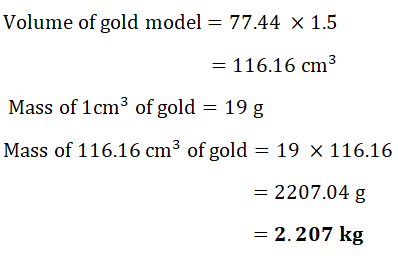 |
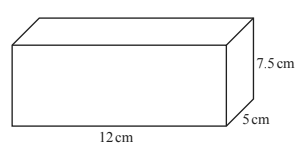
6.Calculate the total surface area of the cuboid.
 (Cambridge Assessment International Education. 0580/22, February/March 2019, Q 10)
(Cambridge Assessment International Education. 0580/22, February/March 2019, Q 10) 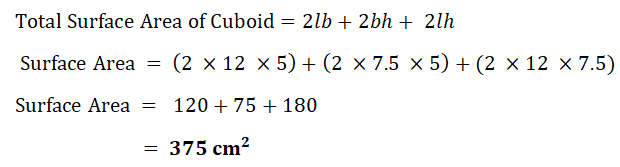 |
7. A cone with height 14.8cm has volume 275cm3.Calculate the radius of the cone.
(The volume, V, of a cone with radius r and height h is V = 1/3πr²h)
(Cambridge Assessment International Education. 0580/22, February/March 2019, Q 12)
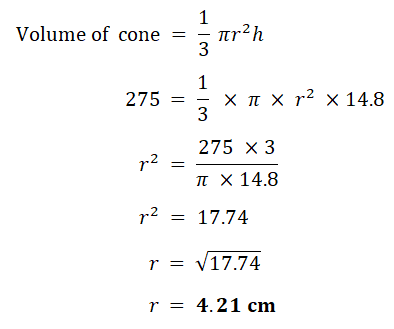 |
8. A pipe is full of water. The cross-section of the pipe is a circle, radius 2.6cm.
Water flows through the pipe into a tank at a speed of 12 centimetres per second.
Calculate the number of litres that flow into the tank in one hour.
(Cambridge Assessment International Education. 0580/22, February/March 2019, Q 18)
 |
9. (a) The lake behind a dam has an area of 55 hectares.
When the gates in the dam are open, water flows out at a rate of 75 000 litres per second.
(i) Show that 90 million litres of water flows out in 20 minutes.
(ii) Beneath the surface, the lake has vertical sides.
Calculate the drop in the water level of the lake when the gates are open for 20 minutes.
Give your answer in centimetres. (1 hectare = 10⁴ m², 1000 litres = 1m³)
(iii) The cross-section of a gate is a sector of a circle with radius 8.5m and angle 76°.
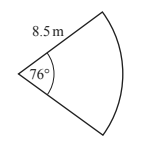
Calculate the perimeter of the sector.
(b) A solid metal cone has radius 10 cm and height 36 cm.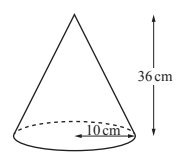
(i) Calculate the volume of this cone.
(The volume, V, of a cone with radius r and height h is V = 1/3πr²h)
(ii) The cone is cut, parallel to its base, to give a smaller cone.
The volume of the smaller cone is half the volume of the original cone.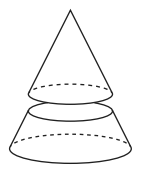
The smaller cone is melted down to make two different spheres.
The ratio of the radii of these two spheres is 1 : 2.
Calculate the radius of the smaller sphere.
(The volume, V, of a sphere with radius r is V = 4/3πr³)
(Cambridge Assessment International Education. 0580/42, October/November 2018, Q 10)
| (a)(i) |  |
| (a)(ii) |  |
| (a)(iii) |  |
| (b)(i) |  |
| (b)(ii) | 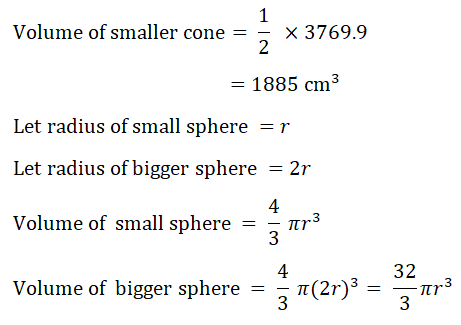 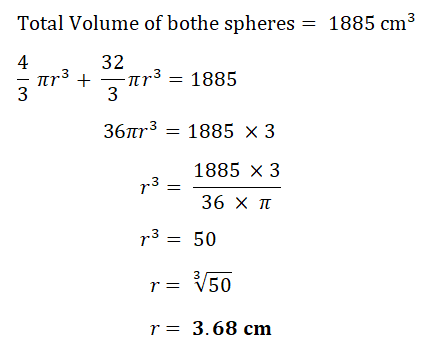 |
10. The diagram shows an equilateral triangle ABC with sides of length 10 cm.
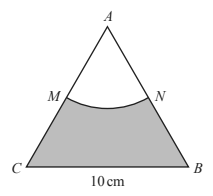
AMN is a sector of a circle, centre A. M is the mid-point of AC.
Work out the area of the shaded region.
(Cambridge Assessment International Education. 0580/22, October/November 2018, Q 21)
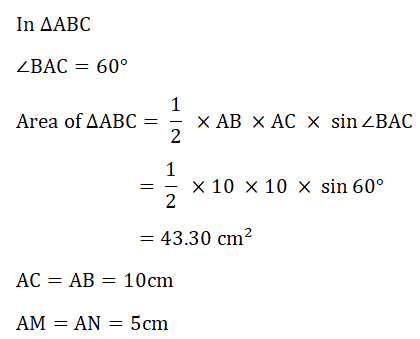  |
11. (c) The perimeter of the design is 29.5cm.
Show that angle COB = 41.2°, correct to 1 decimal place.
(d) Calculate the total area of the design.
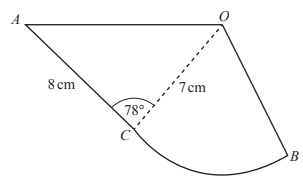
(Cambridge Assessment International Education. 0580/42, May/June 2018, Q 5)
| (c) |   |
| (d) | 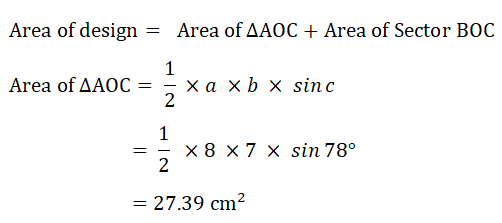  |
12. The diagram shows a solid cuboid with base area 7 cm².
 The volume of this cuboid is 21 cm³.
The volume of this cuboid is 21 cm³.Work out the total surface area.
(Cambridge Assessment International Education. 0580/22, May/June 2018, Q 14)
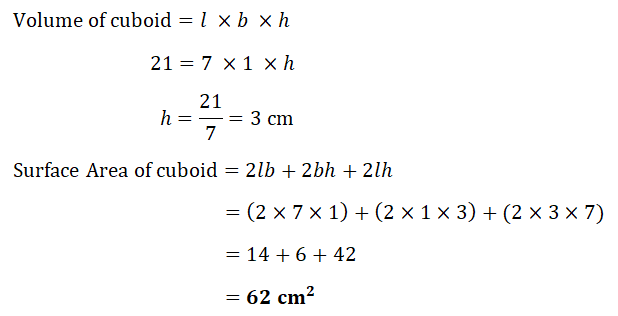 |
13. Find the volume of a cylinder of radius 5 cm and height 8 cm.
Give the units of your answer.
(Cambridge Assessment International Education. 0580/22, May/June 2018, Q 15)
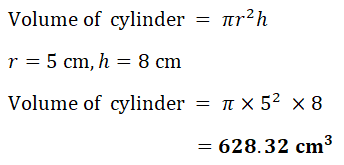 |
14. The vertices of a square ABCD lie on the circumference of a circle, radius 8 cm.
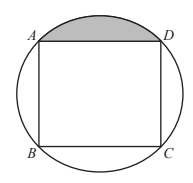 (a) Calculate the area of the square.
(a) Calculate the area of the square.(b) (i) Calculate the area of the shaded segment.
(ii) Calculate the perimeter of the shaded segment.
(Cambridge Assessment International Education. 0580/42, February/March 2018, Q 2)
| (a) | 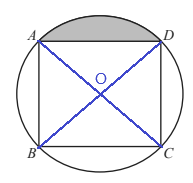  |
| (b)(i) |  |
| (b)(ii) | 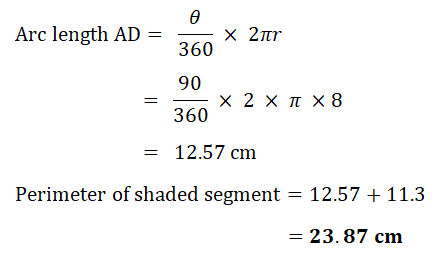 |
15. (a) The diagram shows a solid prism with length 15.2cm.
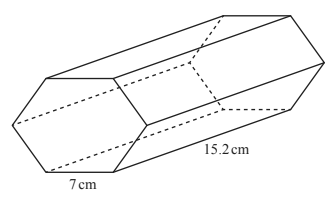
The cross-section of this prism is a regular hexagon with side 7cm.
(i) Calculate the volume of the prism.
(ii) Calculate the total surface area of the prism.
(b) Another solid metal prism with volume 500cm3 is melted and made into 6 identical spheres.
Calculate the radius of each sphere. (The volume, V, of a sphere with radius r is V = 4/3πr³)
(Cambridge Assessment International Education. 0580/42, February/March 2018, Q 5)
| (a)(i) |   |
| (a)(ii) | 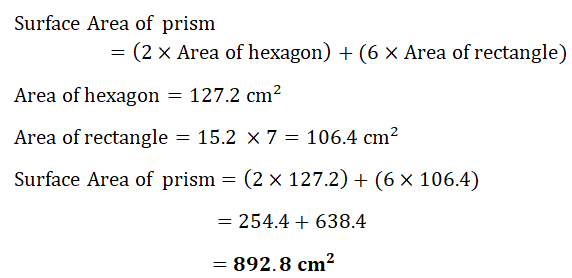 |
| (b) |  |
 (b) Calculate AC.
(b) Calculate AC.(Cambridge Assessment International Education. 0580/22, February/March 2018, Q 16)
| (a) | 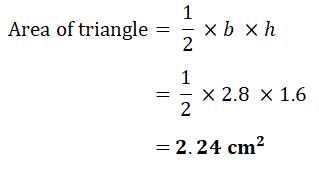 |
| (b) | 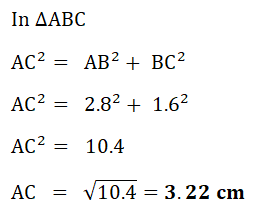 |
17. (a) A sphere of radius r is inside a closed cylinder of radius r and height 2r.
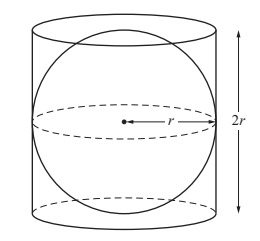 (The volume, V, of a sphere with radius r is V = 4/3πr³)
(The volume, V, of a sphere with radius r is V = 4/3πr³)(i) When r = 8 cm, calculate the volume inside the cylinder which is not occupied by the sphere.
(ii) Find r when the volume inside the cylinder not occupied by the sphere is 36 cm3.
(b) The diagram shows a solid cone with radius 5 cm and perpendicular height 12cm.
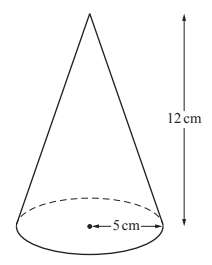 (i) The total surface area is painted at a cost of $0.015 per cm2.
(i) The total surface area is painted at a cost of $0.015 per cm2.Calculate the cost of painting the cone.
(The curved surface area, A, of a cone with radius r and slant height l is A = π r l)
(ii) The cone is made of metal and is melted down and made into smaller solid cones with
radius 1.25 cm and perpendicular height 3 cm.
Calculate the number of smaller cones that can be made.
(Cambridge Assessment International Education. 0580/42, October/November 2017, Q 2)
| (a)(i) |  |
| (a)(ii) | 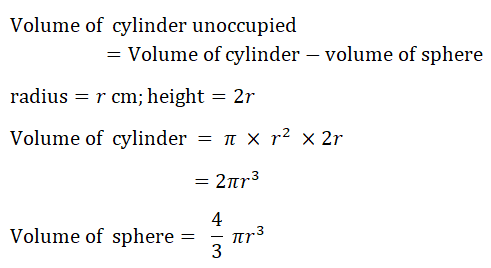 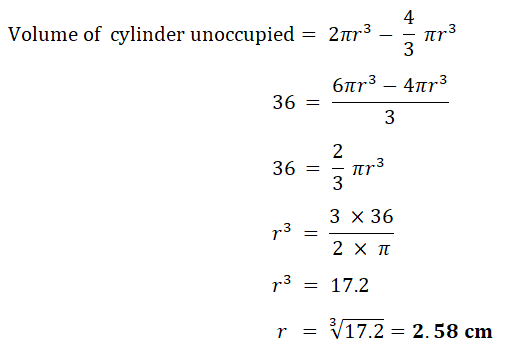 |
| (b)(i) |  |
| (b)(ii) | 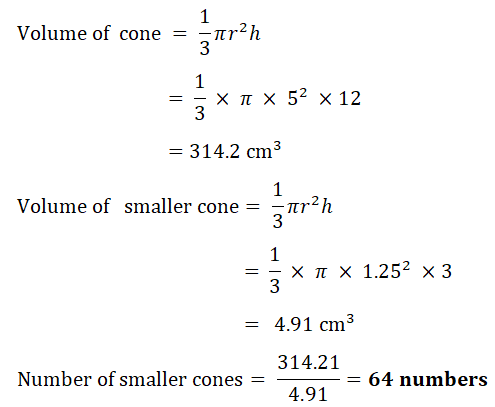 |
18. The diagram shows a sector of a circle, a triangle and a rectangle.
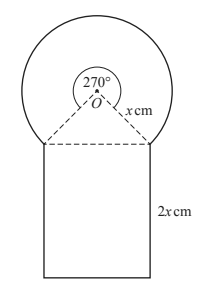 The sector has centre O, radius x cm and angle 270°.
The sector has centre O, radius x cm and angle 270°.The rectangle has length 2x cm.
The total area of the shape is kx² cm².
(a) Find the value of k.
(b) Find the value of x when the total area is 110 cm².
(Cambridge Assessment International Education. 0580/42, October/November 2017, Q 10)
| (a) | 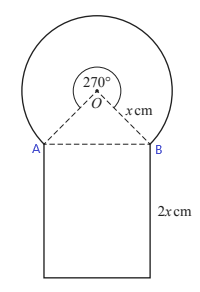   |
| (b) | 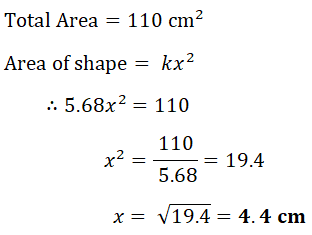 |
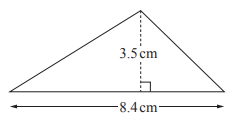
19. The area of a triangle is 528 cm². The length of its base is 33 cm.
Calculate the perpendicular height of the triangle.
(Cambridge Assessment International Education. 0580/22, October/November 2017, Q 7)
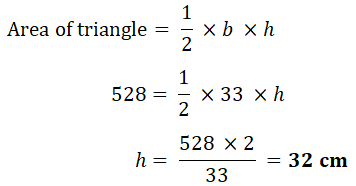 |
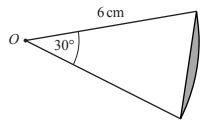
The sector angle is 30°.
The area of the shaded segment is (kπ – c) cm², where k and c are integers.
Find the value of k and the value of c.
(Cambridge Assessment International Education. 0580/22, October/November 2017, Q 23)
 |
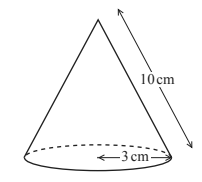 (a) (i) Calculate the curved surface area of the cone.
(a) (i) Calculate the curved surface area of the cone.(The curved surface area, A, of a cone with radius r and slant height l is A = π r l)
(ii) Calculate the perpendicular height of the cone.
(iii) Calculate the volume of the cone.
(The volume, V, of a cone with radius r and height h is V = 1/3πr²h)
(b) The cone is cut along the line OP and is opened out into a sector as shown in the diagram.
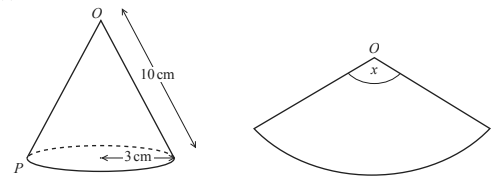 Calculate the sector angle x.
Calculate the sector angle x.(c) The diagram shows the same sector as in part (b).
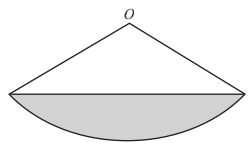 Calculate the area of the shaded segment.
Calculate the area of the shaded segment.(Cambridge Assessment International Education. 0580/42, May/June 2017, Q 5)
| (a)(i) | 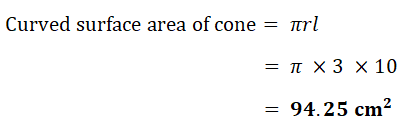 |
| (a)(ii) | 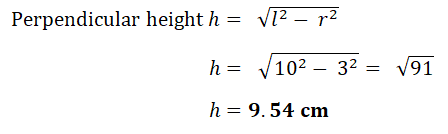 |
| (a)(iii) | 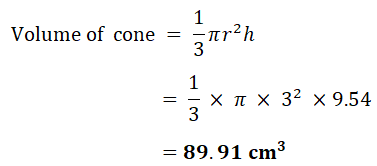 |
| (b) |  |
| (c) |  |
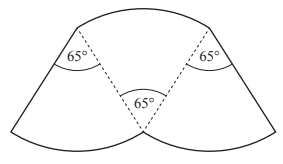 The perimeter of the shape is 20.5cm. Calculate the radius of the circle.
The perimeter of the shape is 20.5cm. Calculate the radius of the circle.(Cambridge Assessment International Education. 0580/42, February/March 2017, Q 8b)
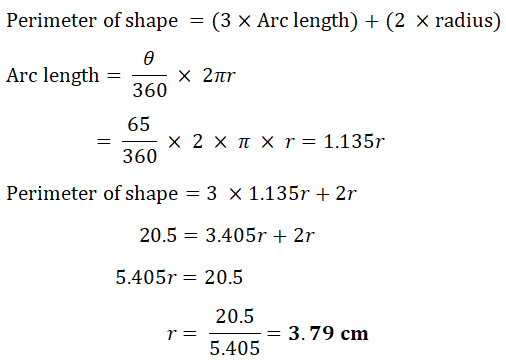 |