1. Water is flowing into an inverted cone of diameter and height 30 cm,
at a rate of 4 liters per minute.
How long in seconds, will it take to fill the cone?
 |
2. A spherical ball is immersed in water contained in a vertical cylinder.
The rise in water level is measured in order to calculate the radius of the spherical balls.
Calculate the radius of the balls in the following cases:
a) Cylinder of radius 10 cm, water level rises 4 cm
b) Cylinder of radius 100 cm, water level rises 8 cm.
| a) |   |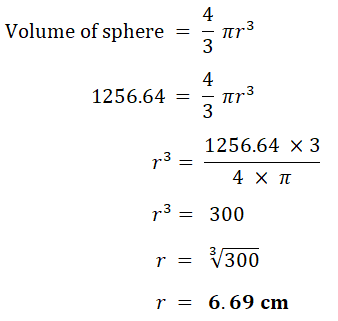
| b) |   |
three adjacent sides.
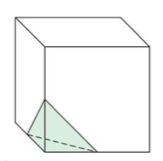Calculate the volume of the piece removed. |  |
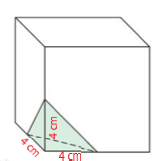4. The cylindrical end of a pencil is sharpened to produce a perfect cone at the end with no
overall loss of length. If the diameter of the pencil is 1 cm, and the cone is of length 2 cm,
calculate the volume of the shavings.
  |
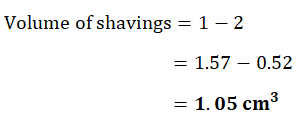Calculate the depth of water in the cone, measured from the vertex.
 |   |
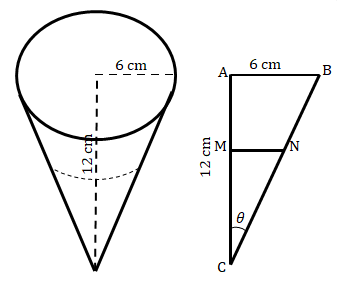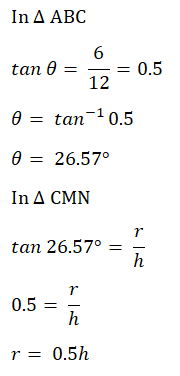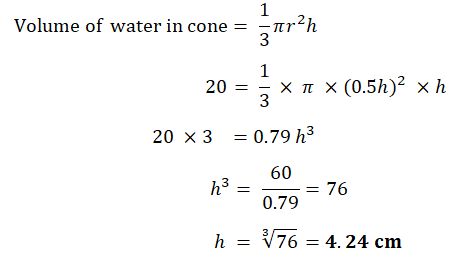6. A frustum is a cone with 'the end chopped off'.
A bucket in the shape of a frustum as shown has diameters of 10 cm and 4 cm
at its ends and a depth of 3 cm.
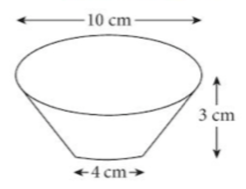Calculate the volume of the bucket.  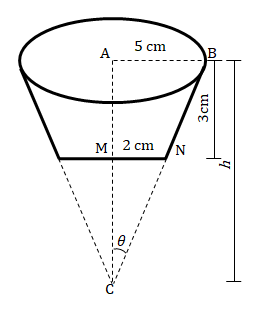| The volume of the bucket(frustum) is basically the volume of cut off portion of cone subtracted from volume of entire cone.   |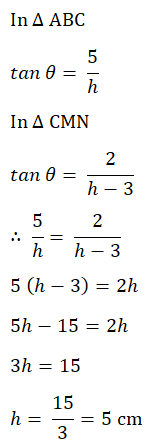
7. The diagram shows a sector of a circle of radius 10 cm.
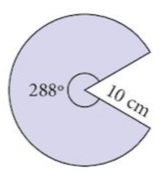
a) Find as a multiple of π, the arc length of the sector.
The straight edges are brought together to make a cone. Calculate:
b) the radius of the base of the cone,
c) the vertical height of the cone.
| a) |  |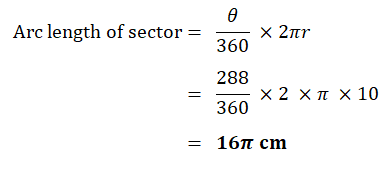
| b) | Circumference of the base of cone is the arc length of sector of circle. |
| c) |   |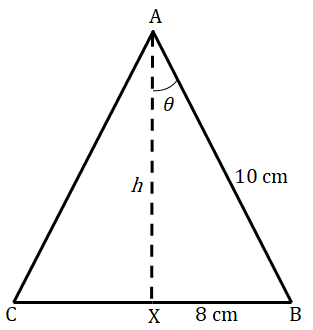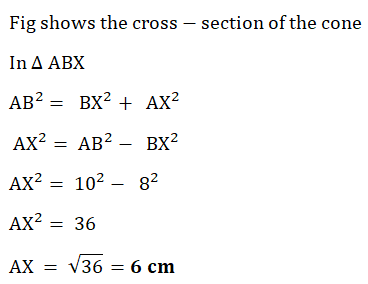
8. A sphere passes through the eight corners of a cube of side 10 cm.
Find the volume of the sphere.
  |   |
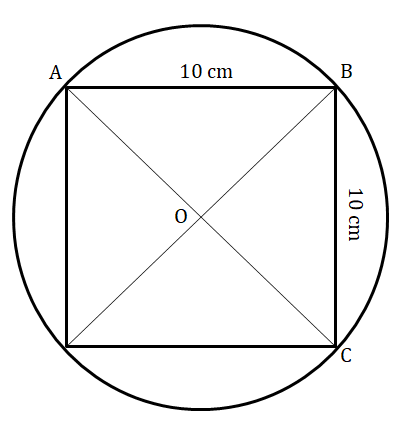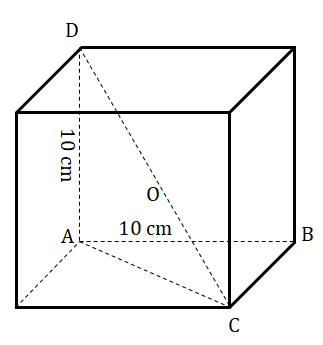9. Find the volume of a tetrahedron of side 20 cm.
(A regular tetrahedron has four equal faces which are equilateral triangle)
Plan of the base of tetrahedron.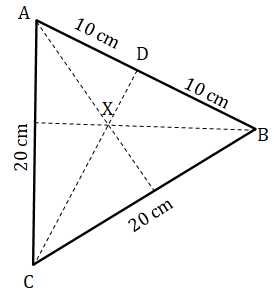 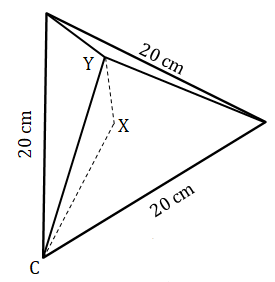 |  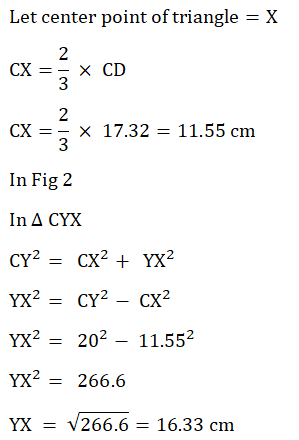 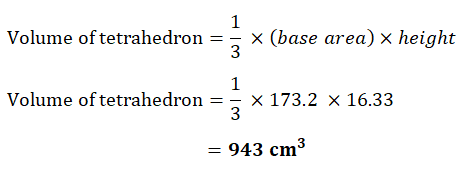 |