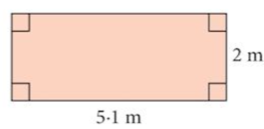
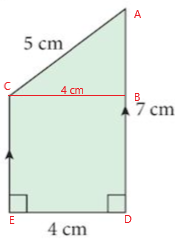
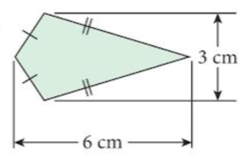
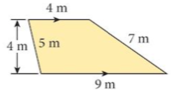
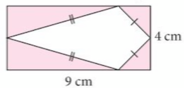
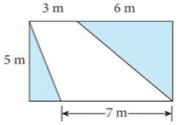
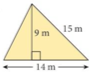
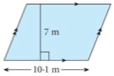
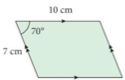
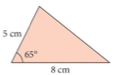
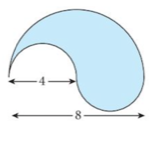
1. Find area of each shape.
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
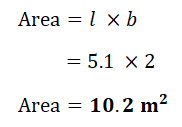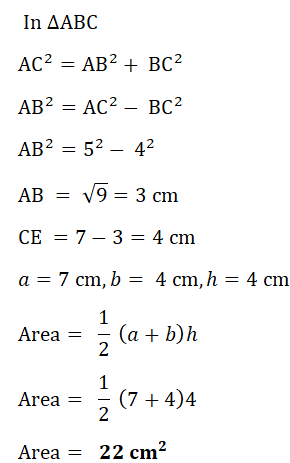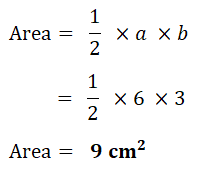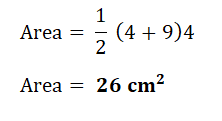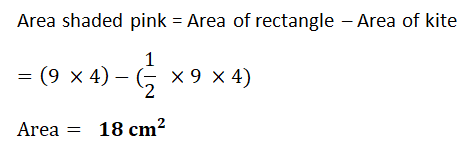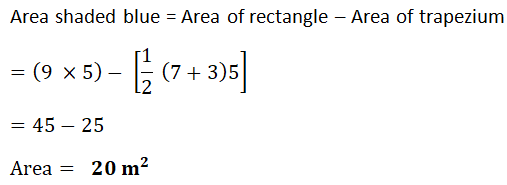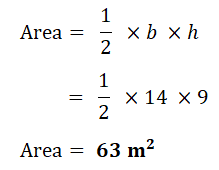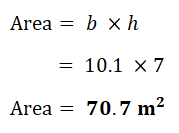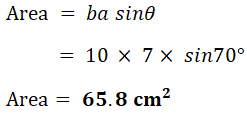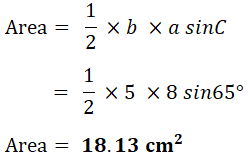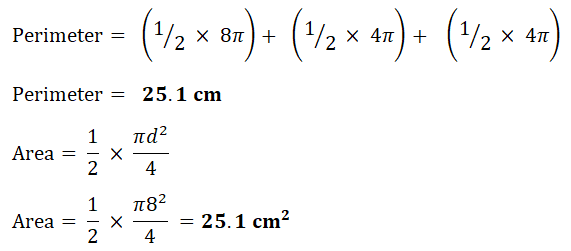2. A trapezium of area 140 sq cm has parallel sides 10 cm apart and one of these sides is 16 cm long.
Find the length of the other parallel side.
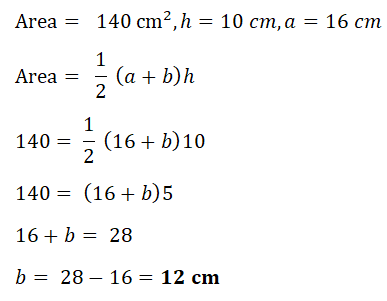
3. A floor 5 m by 20 m is covered by square tiles of side 20 cm.
How many tiles are needed.
| The number of tiles required cab be obtained by dividing the area of floor by the area of one tile Step 1: Find area of floor. Step 2: Find area of one tile Step 3: Divide floor area by tile area.  |
4. A rectangular field, 400 m long, has an area of 6 hectares.
Calculate the perimeter of the field.
| Step 1: Find breadth of the rectangular field. Step 2: Calculate Perimeter  |
5.Find the length of a side of an equilateral triangle of area 10.2 sq m.
 |
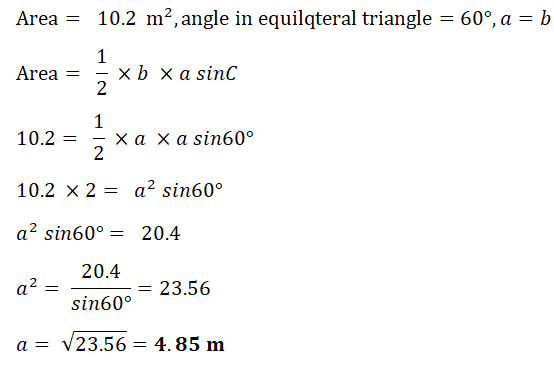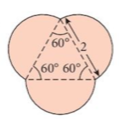
6. A regular hexagon is circumscribed by a circle of radius 3 cm with center O.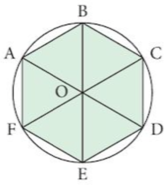
a) What is angle EOD?
b) Find the area of the triangle EOD and hence find area of hexagon ABCDEF.
| a) |  |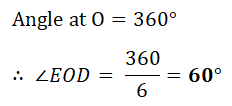
| b) |  |
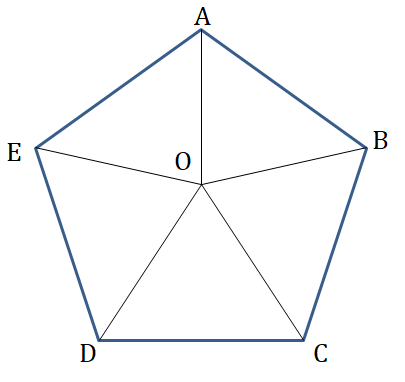
7. The area of a regular pentagon is 600 sq cm.
Calculate the length of one side of the pentagon.
 |   |
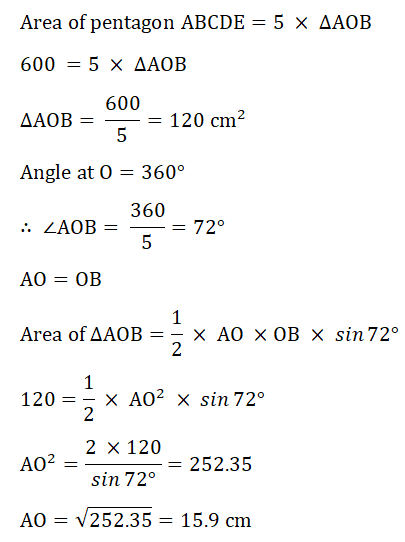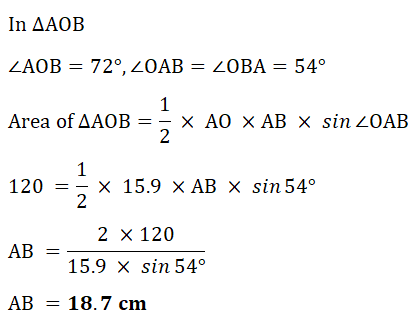8. Discs of radius 4 cm are cut from a rectangular plastic sheet of length 84 cm and width 24 cm.
a) How many complete discs can be cut out?
Find:
b) the total area of the discs cut
c) the area of the sheet wasted.
| a) |  |
| b) |  |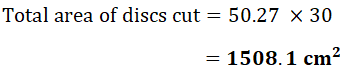
| c) |  |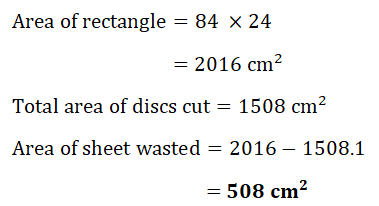
9. A circular pond of radius 6 m is surrounded by a path of width 1 m.
a) Find the area of the path
b) The path is resurfaced with astroturf.
It is bought in packs each containing enough to cover an area of 7 sq m.
How many packs are required?
| a) |  |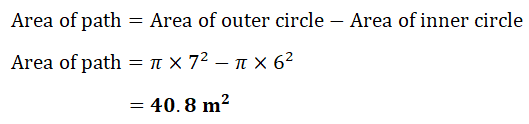
| b) | Each astroturf pack covers an area = 7 sq m. |
10. A golf ball of diameter 1.68 inches rolls a distance of 4 m in a straight line.
How many times does the ball rotate completely?
(1 inch = 2.54 cm)
| Each time the ball rolls completely is one full circumference of the ball Hence Step 1: Calculate circumference of the ball Step 2: Divide it by the total distance rolled to see the number of complete rotations  |
11. A square is inscribed in a circle of radius 7 cm. Find:
a) the area of the square
b) the area shaded blue.
| a) |   |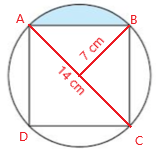
| b) | Area of square subtracted from the area of circle will give us the area of the four sectors. This can be divided by 4 to give us the area of portion shaded blue.  |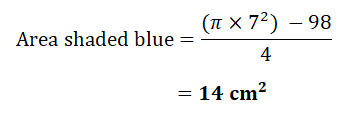
12. The diagram shows a circle inside a rectangle.
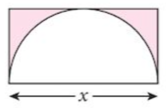The pink shaded area is 84 sq cm. Find x.
  |
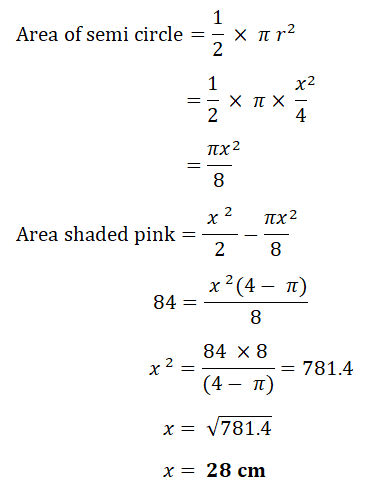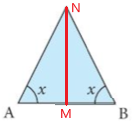
13.The semi-circle and the isosceles triangle have the same base AB.
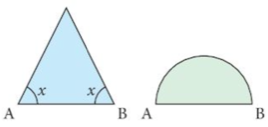They have the same area. Find the angle x.
 |   |
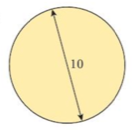
14.The diameter of a circle is given as 10 cm, correct to the nearest cm.
Calculate:
a) the maximum possible circumference
b) the minimum possible area of the circle consistent with this data.
| a) |  |
| b) |  |