Source: Complete International Mathematics For Cambridge IGCSE - David Rayner, Jim Fenson
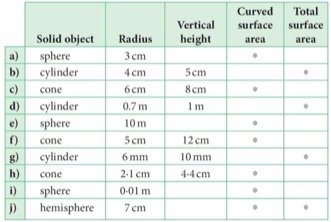
| a) | Sphere | 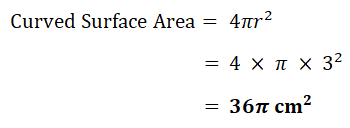 |
| b) | Cylinder | 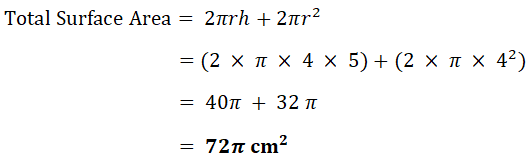 |
| c) | Cone | 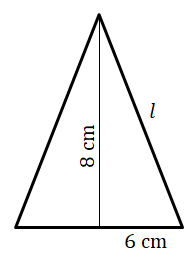  |
| d) | Cylinder | 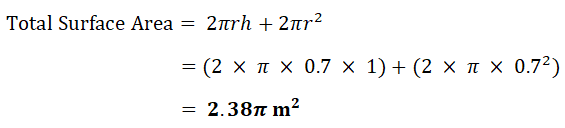 |
| e) | Sphere | 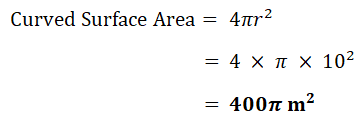 |
| f) | Cone | 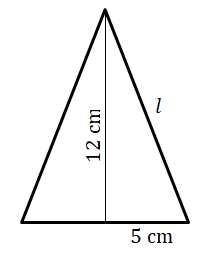 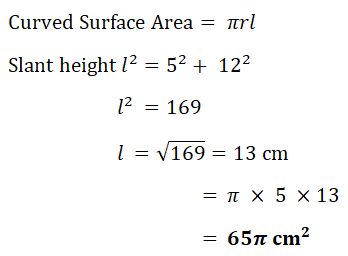 |
| g) | Cylinder | 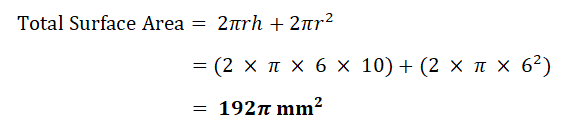 |
| h) | Cone | 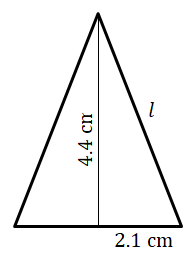  |
| i) | Sphere | 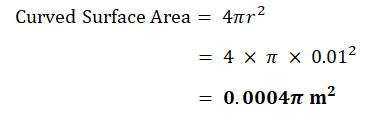 |
| j) | Hemisphere |  |
2. A solid wooden cylinder of height 8 cm and radius 3 cm is standing vertically.
It is then cut in two along a vertical plane of symmetry.
Calculate the surface area of the two pieces.
| Each cut piece has the following surfaces: 1. A rectangle (along the cut plane) 2. Two semi-circles(base and top) 3. Half the circular face of the cylinder.   |
3. A tin of paint covers a surface area of 60 cm² and costs $4.50.
Find the cost of painting the outside surface of a hemispherical dome of radius 50 m.
(Just the curved part)
 |
4. Find the surface area of a sphere of volume 28 cm³.
 |
5. A golf ball has a diameter of 4.1 cm and the surface has 150 dimples of radius 2 mm.
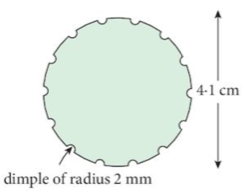
Calculate the total surface area which is exposed to the surroundings.
(assume the dimples are hemispherical)
| The golf ball can be considered a sphere. The dimples can be considered holes cut out on the surface of the sphere. In addition the surface area of the dimples have to be calculated.   |
6. A cone of radius 3 cm and slant height 6 cm is cut into four identical pieces.
Calculate the total surface area of the four pieces.
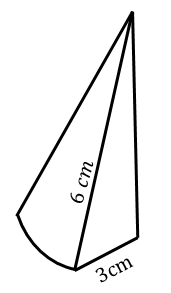 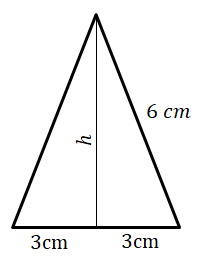 |    |