Angle ACD = x° and angle OAB = 2x°.
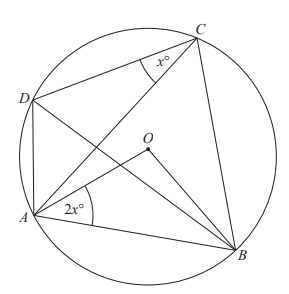
Find an expression, in terms of x, in its simplest form
for
(a) angle AOB,
(b) angle ACB,
(c) angle DAB.
(Cambridge Assessment International Education. 0580/22, October/November 2019, Q 19)
| (a) |  |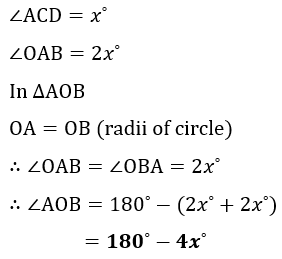
| (b) |  |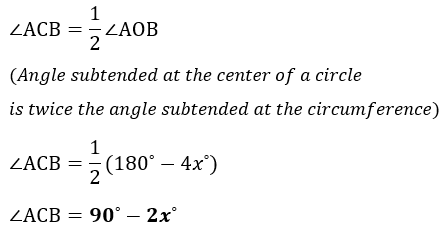
| (c) |  |
2. The diagram shows a circle with diameter PQ.
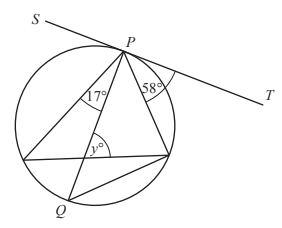
Find the value of y.
(Cambridge Assessment International Education. 0580/42, May/June 2019, Q 2b)
 |   |
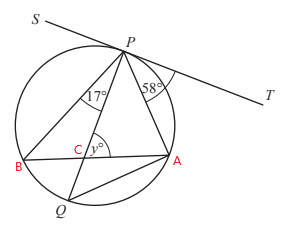3. A, B and C are points on the circle, center O.
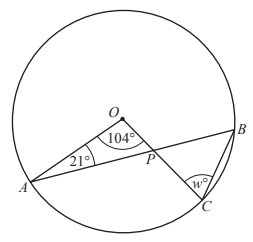AB and OC intersect at P.
Find the value of w.
(Cambridge Assessment International Education. 0580/22, February/March 2019, Q 15)
  |
4. In the diagram, A, B, C and D lie on the circle, centre O.
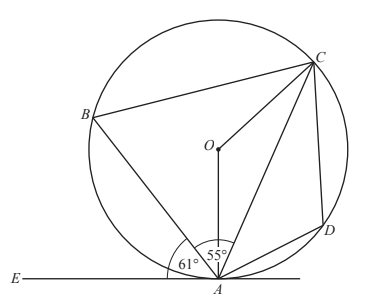
EA is a tangent to the circle at A.
Angle EAB = 61° and angle BAC = 55°.
(a) Find angle BAO.
(b) Find angle AOC.
(c) Find angle ABC.
(d) Find angle CDA.
(Cambridge Assessment International Education. 0580/42, October/November 2018, Q 7)
| (a) |  |
| (b) |  |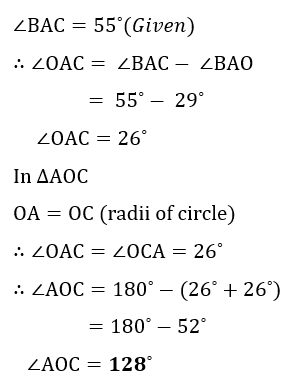
| (c) |  |
| (d) |  |
5. A, B, C, D and E lie on the circle, centre O.
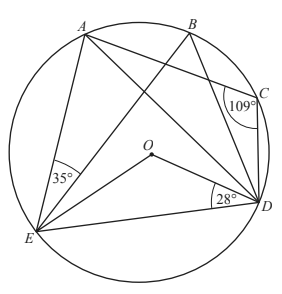
Angle AEB = 35°, angle ODE = 28° and angle ACD = 109°.
(i) Work out the following angles, giving reasons for your answers.
(a) Angle EBD
(b) Angle EAD
(ii) Work out angle BEO.
(Cambridge Assessment International Education. 0580/42, May/June 2018, Q 9a)
| 5(i)a |   |
| 5(i)b |  |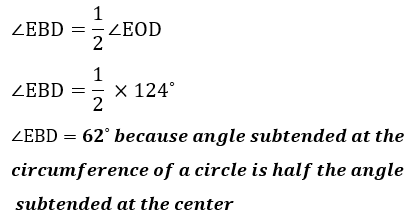
| 5(ii) |  |
6. A, B, C and D are points on the circle, center O.
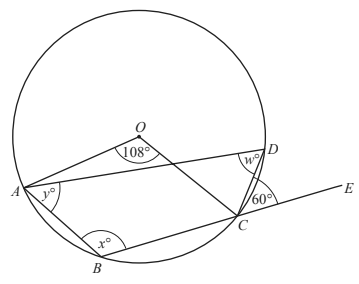BCE is a straight line.Angle AOC = 108° and angle DCE = 60°.
Calculate the values of w, x and y.
(Cambridge Assessment International Education. 0580/22, October/November 2017, Q 22)
   |
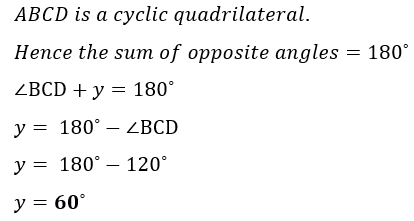7. A, B, C, D and E lie on the circle.
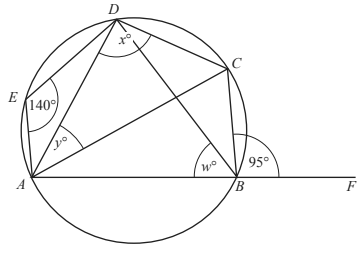AB is extended to F.Angle AED = 140° and angle CBF = 95°.
Find the values of w, x and y.
(Cambridge Assessment International Education. 0580/22, May/June 2017, Q 26)
   |
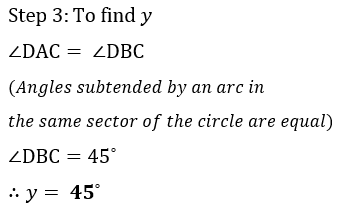8. The diagram shows points A, B, C and D on the circumference of a circle, centre O.
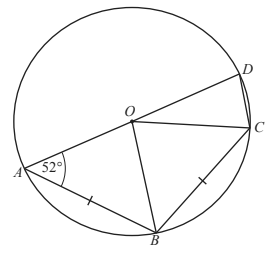AD is a straight line, AB = BC and angle OAB = 52°.Find angle ADC.
  |
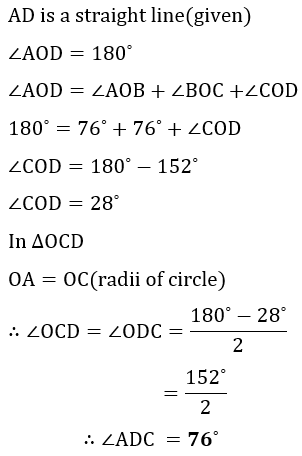(c) The diagram shows points P, Q, R and S on the circumference of a circle, centre O.
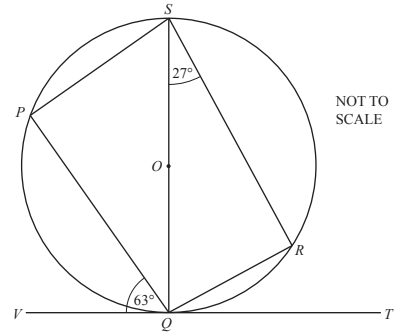
VT is the tangent to the circle at Q.
Complete the statements.
(i) Angle QPS = angle QRS = ................ ° because ................
(ii) Angle SQP = ................ ° because .....................................
(iii) Part (c)(i) and part (c)(ii) show that
the cyclic quadrilateral PQRS is a ...........................................
(Cambridge Assessment International Education. 0580/42, February/March 2017, Q 6b &6c)
| (c)(i) | Angle QPS = angle QRS = 90° because angle in a semi circle is a right angle |
| (c)(ii) |  Angle SQP = 27° because angle between a tangent and the radius drawn to thepoint of contact is 90° |
| (c)(iii) |   Part (c)(i) and part (c)(ii) show that the cyclic quadrilateral PQRS is a rectangle |